Raportul Dintre Catetele Unui Triunghi Dreptunghic Este 5 6

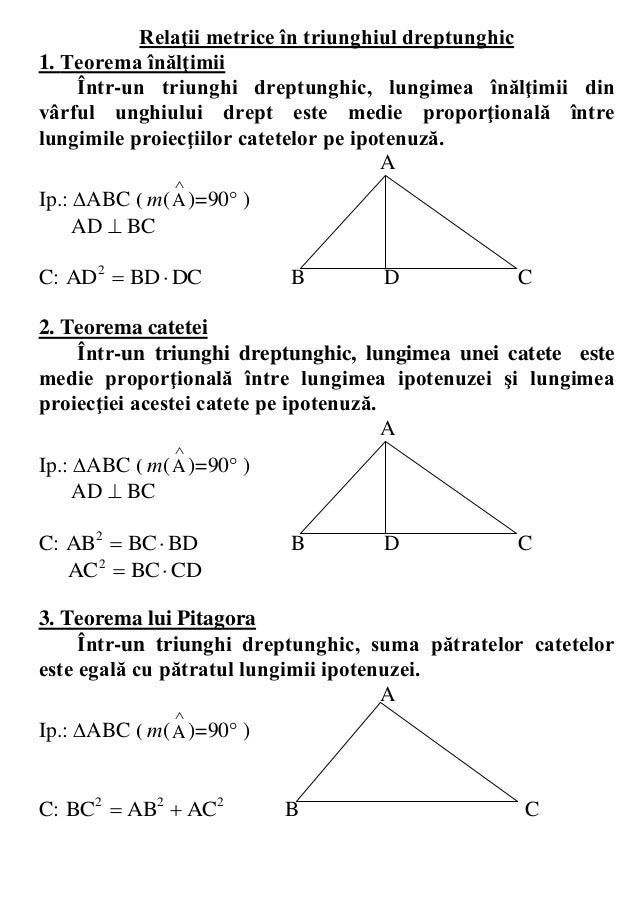
Teorema înălțimii într un triunghi dreptunghic lungimea înălțimii corespunzătoare ipotenuzei este egală cu media geometrică dintre proiecțiile catetelor pe ipotenuză.

Raportul dintre catetele unui triunghi dreptunghic este 5 6. Sinusul cosinusul tangenta si cotangenta unui unghi ascutit pe examenultau ro. Iar daca aplicam si prima formula in triunghiului dreptunghic obtinem ca pentru ca stim inca din clasa a vi a ca intr un triunghi dreptunghic putem duce trei inaltimi doua dintre ele coincid cu cele doua catete iar cea de a treia inaltime este ad cea corespunzatoare ipotenuzei in cazul nostru bc. Trebuie doar sa cunoasca valoarea tangentei de care este adica aproximativ 1 73. știind că înălțimea corespunzătoare ipotenuzei are lungimea de 8 dm aflați lungimea ipotenuzei triunghiului dreptunghic.

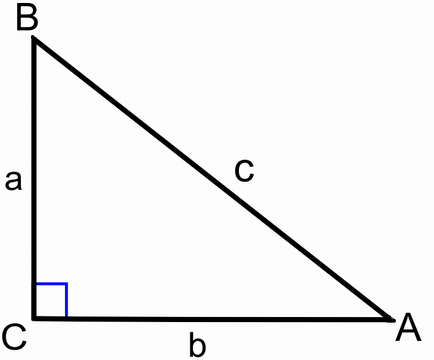
Problema 2 aria unui triunghi dreptunghic este de 40 dm. Obtinem si de aici deci latimea raului este de aproximativ 60 x 1 73 103 8 m. Dacă într un triunghi isoscel unghiurile alăturate bazei au măsura de 60 atunci triunghiul este echilateral. Latura c este ipotenuza iar laturile a și b sunt catetele.

H δ d r e p t u n g h i c c a t e t a 1 c a t e t a 2 i p o t e n u z ă. Set pentru ascutirea lantului husqvarn. Raportul dintre catetele unui triunghi dreptunghic este 5 6 iar ip 2radical din 61 aflati catetele si inaltimea triunghiului dreptunghic explicații va 49279. în triunghiul dreptunghic fiecare catetă este egală cu media geometrică dintre ipotenuză și proiecția catetei pe ipotenuză.

Bisectoarea este semidreapta interioară cu originea în vârful unghiului care împarte unghiul în 2 unghiuri congruente. Raportul dintre catetele unui triunghi dreptunghic este 5 pe 6 iar ipotenuza este 2radical din 61 cm aflati catetele si inaltimea triunghiului dreptunghic 522. în geometria plană un triunghi dreptunghic este triunghiul care are un unghi drept π 2 radiani sau 90. Problema 3 aflați aria unui triunghi dreptunghic isoscel știind că lungimea ipotenuzei triunghiului este de 12 cm.

Aflati mai multe despre notiunile de trigonometrie in triunghiul dreptunghic. Oricare ar fi trei numere pozitive a b c astfel încât a2 b2 c2 există un triunghi cu laturi de lungimi a b c iar unghiul dintre laturile de lungimi a și b va fi drept deși teorema se atribuie astăzi filozofului și matematicianului grec antic pitagora care a trăit în secolul al șaselea îdc se știe cu siguranță că a fost cunoscută de mai.